Let's summarize what have been told up until now.
Complex sinusoid $csin(k,n)$ is used by DFT and IDFT to convert between signal representations.
$$csin(k,n) = e^{j*2\pi * k/N * n}$$
$k$-th complex sinusoid does k cycles (loops) over N+1 samples.
$n$ is a sample number of complex sinusoid.
$csin(k,n)$ for $k=2$ and $n=0,1,..,N-1$ plotted in 3D looks like
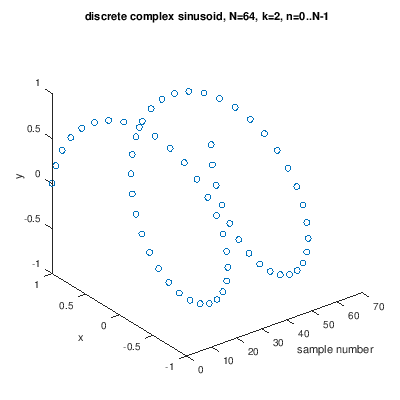
For computing values of complex sinusoids we use important formula called Euler's formula which states
$$e^{j\phi} = cos(\phi) + j*sin(\phi)$$
For complex sinusoids used in DFT and IDFT this becomes (they differ by minus sign in exponent)
$$e^{-j*2\pi*k/N*n} = cos(2\pi*k/N*n) - j*sin(2\pi*k/N*n)$$
$$e^{j*2\pi*k/N*n} = cos(2\pi*k/N*n) + j*sin(2\pi*k/N*n)$$
Let $x = (x_0, x_1, .., x_{N-1})$ be an input signal with $N$ samples.
Discrete Fourier Transform (DFT) is a function that takes samples of a signal and returns scaling coefficents of complex sinusoids.
$$DFT(x) = y = (y_0, y_1, y_2, ..., y_{N-1})$$
$$y_k = \sum_{n=0}^{N-1}x_n*e^{-j*2\pi*k/N*n}$$
Inverse Discrete Fourier Transform (IDFT) is a function that takes scaling coefficents of complex sinusoids and returns samples of the signal.
$$IDFT(y) = x = (x_0, x_1, x_2, ..., x_{N-1})$$
$$x_n = \frac{1}{N} \sum_{k=0}^{N-1}y_k * e^{j*2\pi*k/N*n}$$
Signal $x$ which is sampled in time or space is called time domain signal.
Signal $y$ which contains scaling coefficents is called frequency domain signal.