Purpose of this article is to explain what is MDCT and how to use it. It does not go deep into details why MDCT works.
At the end of the article there is available implementation of MDCT.
To be able to follow this article you should know:
Quick navigation menu
Modified Discrete Cosine Transform (MDCT) is a transform that changes representation of a signal. In this manner it reminds Discrete Fourier Transform, but that is the only similarity. MDCT works only with real values and uses sinusoids instead of complex exponentials to represent signal.
MDCT is mainly used in audio compression eg. in MP3.
MDCT is unusual between transforms in two ways
You will see later where these properties fit and how to restore original signal from values of inverse MDCT.
MDCT consists of forward and inverse transform
Forward MDCT
$$y_k = \sum_{n=0}^{2N-1}x_n\cos(2\pi\frac{k+\frac{1}{2}}{2N}(n+\frac{1}{2}+\frac{N}{2}))$$
Inverse MDCT
$$z_n = \frac{1}{N}\sum_{k=0}^{N-1}y_k\cos(2\pi\frac{k+\frac{1}{2}}{2N}(n+\frac{1}{2}+\frac{N}{2}))$$
Because forward MDCT takes 2N samples but gives only N values it loses some information. This is why inverse MDCT gives $z_n$, not $x_n$ as these values are not the same.
Time to see how to calculate MDCT by hand.
Let signal $x=(1,3,5,7)$,
length(x)=4, so 2N=4, N=2, n=0..3, k=0..1
$$y_0 = \sum_{n=0}^{2N-1}x_n\cos(2\pi\frac{0+\frac{1}{2}}{2N}(n+\frac{1}{2}+\frac{N}{2})) = \\ \sum_{n=0}^{4-1}x_n\cos(2\pi\frac{0+\frac{1}{2}}{4}(n+\frac{1}{2}+\frac{2}{2})) = \sum_{n=0}^{3}x_n\cos(2\pi\frac{1}{8}(n+\frac{3}{2})) = \\ x_0\cos(2\pi\frac{1}{8}(0+\frac{3}{2})) + x_1\cos(2\pi\frac{1}{8}(1+\frac{3}{2})) + x_2\cos(2\pi\frac{1}{8}(2+\frac{3}{2})) + x_3\cos(2\pi\frac{1}{8}(3+\frac{3}{2})) = \\ 1 * \cos(2\pi\frac{3}{16}) + 3 * \cos(2\pi\frac{5}{16}) + 5 * \cos(2\pi\frac{7}{16}) + 7 * \cos(2\pi\frac{9}{16}) = \\ 1 * 0.38268 + 3 * (-0.38268) + 5 * (-0.92388) + 7 * (-0.92388) = -11.852 $$
$$y_1 = \sum_{n=0}^{2N-1}x_n\cos(2\pi\frac{1+\frac{1}{2}}{2N}(n+\frac{1}{2}+\frac{N}{2})) = \\ \sum_{n=0}^{3}x_n\cos(2\pi\frac{1+\frac{1}{2}}{4}(n+\frac{1}{2}+\frac{2}{2})) = \sum_{n=0}^{3}x_n\cos(2\pi\frac{3}{8}(n+\frac{3}{2})) = \\ x_0\cos(2\pi\frac{3}{8}(0+\frac{3}{2})) + x_1\cos(2\pi\frac{3}{8}(1+\frac{3}{2})) + x_2\cos(2\pi\frac{3}{8}(2+\frac{3}{2})) + x_3\cos(2\pi\frac{3}{8}(3+\frac{3}{2})) = \\ 1 * \cos(2\pi\frac{9}{16}) + 3 * \cos(2\pi\frac{15}{16}) + 5 * \cos(2\pi\frac{21}{16}) + 7 * \cos(2\pi\frac{27}{16}) = \\ 1 * (-0.92388) + 3 * 0.92388 + 5 * (-0.38268) + 7 * (-0.38268) = -2.7444 $$
Summarizing: y = mdct(x) = [-11.852, -2.7444].
$$z_0 = \frac{1}{N}\sum_{k=0}^{N-1}y_k\cos(2\pi\frac{k+\frac{1}{2}}{2N}(0+\frac{1}{2}+\frac{N}{2})) = \\ \frac{1}{2}\sum_{k=0}^{2-1}y_k\cos(2\pi\frac{k+\frac{1}{2}}{4}(0+\frac{1}{2}+\frac{2}{2})) = \frac{1}{2}\sum_{k=0}^{1}y_k\cos(2\pi\frac{k+\frac{1}{2}}{4} * \frac{3}{2}) = \\ \frac{1}{2}( y_0\cos(2\pi\frac{0+\frac{1}{2}}{4} * \frac{3}{2}) + y_1\cos(2\pi\frac{1+\frac{1}{2}}{4} * \frac{3}{2}) ) = \\ \frac{1}{2}( -11.852 * \cos(2\pi\frac{3}{16}) + (-2.7444) * \cos(2\pi\frac{9}{16}) = -1.0 $$
$$z_1 = \frac{1}{N}\sum_{k=0}^{N-1}y_k \cos(2\pi\frac{k+\frac{1}{2}}{2N}(1+\frac{1}{2}+\frac{N}{2})) = 1.0 $$
$$z_2 = \frac{1}{N}\sum_{k=0}^{N-1}y_k \cos(2\pi\frac{k+\frac{1}{2}}{2N}(2+\frac{1}{2}+\frac{N}{2})) = 6.0 $$
$$z_3 = \frac{1}{N}\sum_{k=0}^{N-1}y_k \cos(2\pi\frac{k+\frac{1}{2}}{2N}(3+\frac{1}{2}+\frac{N}{2})) = 6.0 $$
In short: z = imdct(y) = [-1.0, 1.0, 6.0, 6.0]
You should try to compute MDCT yourself. Here are some example values you can use for calculations and to check your result.
x=[10, 2, 7, 9]
length(x)=4, 2N=4, N=2, n=0..3, k=0..1
y = mdct(x) = [-11.72, -13.51]
z = imdct(y) = [4.00, -4.00, 8.00, 8.00]
Usage of MDCT is not as simple as using forward and inverse transform. It consists of following steps:
In short:
Let's see how it is done using some signal.
Let signal $s = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]$
length(s) = 16
Let's divide signal into overlapping blocks with 8 samples each
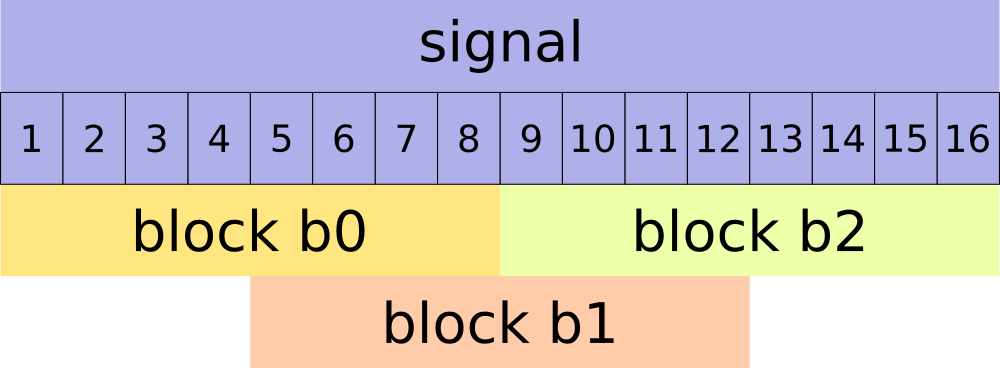
b0 = [1, 2, 3, 4, 5, 6, 7, 8]
b1 = [5, 6, 7, 8, 9, 10, 11, 12]
b2 = [9, 10, 11, 12, 13, 14, 15, 16]
First half of block b1 is the same as second half of block b0.
Fist half of block b2 is the same as second half of block b1.
This is what it means that blocks shall overlap.
In MDCT every block shall overlap exactly half of previous block. If overlap is less than half of block then original signal cannot be restored.
It is also common to say that MDCT uses overlapping window functions to divide signal into overlapping blocks. In this context a window function takes whole signal and returns a single block. From the use of window functions blocks may also be called windows.
To compute forward MDCT for a signal divide signal into blocks b0, b1, b2, .., and calculate MDCT for each block separately.
y_b0 = mdct(b0) = [-25.42 , -4.78 , 4.11 , 3.17]
y_b1 = mdct(b1) = [-39.92 , -9.87 , 7.51 , 6.06]
y_b2 = mdct(b2) = [-54.42 , -14.96 , 10.91 , 8.94]
To restore signal from MDCT first compute inverse MDCT from y_bx values.
z_b0 = imdct(y_b0) = [-1.50, -0.50, 0.50, 1.50, 6.50, 6.50, 6.50, 6.50]
z_b1 = imdct(y_b1) = [-1.50, -0.50, 0.50, 1.50, 10.50, 10.50, 10.50, 10.50]
z_b2 = imdct(y_b2) = [-1.50, -0.50, 0.50, 1.50, 14.50, 14.50, 14.50, 14.50]
When dividing original signal s into blocks, each block was overlapped. Now is the time to use this. Add values of z_bx where original blocks were overlapped ie. second half of z_b0 to fist half of z_b1, second half of z_b1 to first half of z_b2.
z_b0[4] + z_b1[0] = 6.50 + (-1.50) = 5.0
z_b0[5] + z_b1[1] = 6.50 + (-0.50) = 6.0
z_b0[6] + z_b1[2] = 6.50 + 0.50 = 7.0
z_b0[7] + z_b1[3] = 6.50 + 1.50 = 8.0
z_b1[4] + z_b2[0] = 10.50 + (-1.50) = 9.0
z_b1[5] + z_b2[1] = 10.50 + (-0.50) = 10.0
z_b1[6] + z_b2[2] = 10.50 + 0.50 = 11.0
z_b1[7] + z_b2[3] = 10.50 + 1.50 = 12.0
You can see clearly that these are the values from the middle of the original signal s.
It is not possible to restore original values of s from beginning and end of s without adding overlapped blocks.
To restore those values just add a few zeros to the start and end of s, divide signal into new overlapped blocks and follow the procedure. Following example illustrates this.
Let s = [12, 1, 9, 4, 5, 13, 14, 15, 10, 3, 7, 6, 16, 11, 2, 8].
length(s) = 16
This time we want to restore whole signal. We divide signal into blocks of 8 samples and each block overlaps 4 samples. So let's add 4 zeros to the beginning and the end of s. This way all values from signal s will have overlapped blocks and thus every value can be restored.
s0 = [0, 0, 0, 0, 12, 1, 9, 4, 5, 13, 14, 15, 10, 3, 7, 6, 16, 11, 2, 8, 0, 0, 0, 0].
It does not matter if you choose 0 or other value to extend signal. It is just that 0 is a simple, nonmagical value.
Divide s0 into overlapped blocks of 8 values.
b0 = [0, 0, 0, 0, 12, 1, 9, 4]
b1 = [12, 1, 9, 4, 5, 13, 14, 15]
b2 = [5, 13, 14, 15, 10, 3, 7, 6]
b3 = [10, 3, 7, 6, 16, 11, 2, 8]
b4 = [16, 11, 2, 8, 0, 0, 0, 0]
Compute forward MDCT of each block.
y_b0 = mdct(b0) = [-23.11, -5.19, 10.14, 6.94]
y_b1 = mdct(b1) = [-40.23, -21.95, -0.48, 20.34]
y_b2 = mdct(b2) = [-28.86, 5.17, 7.35, -0.40]
y_b3 = mdct(b3) = [-31.26, -7.83, 13.77, 18.05]
y_b4 = mdct(b4) = [6.20, -12.85, 9.04, -2.18]
Compute inverse MDCT of y_bx.
z_b0 = imdct(y_b0) = [-0.00, 0.00, -0.00, 0.00, 8.00, 5.00, 5.00, 8.00]
z_b1 = imdct(y_b1) = [4.00, -4.00, 4.00, -4.00, 10.00, 13.50, 13.50, 10.00]
z_b2 = imdct(y_b2) = [-5.00, -0.50, 0.50, 5.00, 8.00, 5.00, 5.00, 8.00]
z_b3 = imdct(y_b3) = [2.00, -2.00, 2.00, -2.00, 12.00, 6.50, 6.50, 12.00]
z_b4 = imdct(y_b4) = [4.00, 4.50, -4.50, -4.00, 0.00, 0.00, -0.00, 0.00]
Add overlapped blocks to restore original values.
z_b0[4] + z_b1[0] = 8.00 + 4.00 = 12.00
z_b0[5] + z_b1[1] = 5.00 + (-4.00) = 1.00
z_b0[6] + z_b1[2] = 5.00 + 4.00 = 9.00
z_b0[7] + z_b1[3] = 8.00 + (-4.00) = 4.00
z_b1[4] + z_b2[0] = 10.00 + (-5.00) = 5.00
z_b1[5] + z_b2[1] = 13.50 + (-0.50) = 13.00
z_b1[6] + z_b2[2] = 13.50 + 0.50 = 14.00
z_b1[7] + z_b2[3] = 10.00 + 5.00 = 15.00
z_b2[4] + z_b3[0] = 8.00 + 2.00 = 10.00
z_b2[5] + z_b3[1] = 5.00 + (-2.00) = 3.00
z_b2[6] + z_b3[2] = 5.00 + 2.00 = 7.00
z_b2[7] + z_b3[3] = 8.00 + (-2.00) = 6.00
z_b3[4] + z_b4[0] = 12.00 + 4.00 = 16.00
z_b3[5] + z_b4[1] = 6.50 + 4.50 = 11.00
z_b3[6] + z_b4[2] = 6.50 + (-4.50) = 2.00
z_b3[7] + z_b4[3] = 12.00 + (-4.00) = 8.00
You can download example implementation of MDCT and IMDCT written in C.
It also comes with a simple makefile.
The file contains simple MDCT and IMDCT implementations and usage as well as usage of MDCT on a divided signal and how to restore it. The implementation is heavy commented.
All code written here is licensed under Creative Commons Zero license, whose full text can be found at https://creativecommons.org/publicdomain/zero/1.0/. It basically means that you can do with the code whatever you like without asking for any permissions.
Article written 16.03.2017